학습목표
1. 그래프 정의하기
2. 그래프 그리는 방법 연습하기
3. 그래프 클래스 구분하기
Warm-up
문제) 과리니의 퍼즐 : 흰색/검은색 체스 나이트의 위치 바꾸기
문제) 한붓그리기 - 쾨니히스베르크 다리 한 번 씩만 건너기
해설) 오일러의 길 : 시작점과 끝점 가운데 있는 지점들을 빼고 모든 지점이 짝수여야 함
그래프
ex. 항공 그래프, 페이스북 그래프, 인용 그래프, 링크드 오픈 데이터, 생물학, 생화학 분야 등
-> 네비게이션(두 지점 사이의 최단 거리 찾는 알고리즘)
-> 구글 검색(PageRank 페이지에 점수와 순위를 부여해 관련 링크만 보도록 함)
-> 게임, 게놈, GSM, 컴퓨터 칩
An isolated vertex forms a component
분리된 꼭짓점이 구성요소를 형성한다.
1. 꼭짓점의 차수 : 입사 모서리의 수, 이웃한 개수의 수, deg(v), 최대 각도
차수가 0인 꼭짓점은 '분리된 꼭짓점'
모든 꼭짓점의 차수가 같으면 일반 그래프라고 함(regular graph)
모든 꼭짓점의 차수가 k면 k-regular graph
2. walk 모서리, path 경로(동일한 꼭짓점 갈 수 있음) simple path(이미 간 꼭짓점 갈 수 없음)
cycle 첫번째와 마지막 꼭짓점이 같은 경로
3. connectivity 연결성 : 모든 꼭짓점 사이에 연결된 경로가 있을 경우
connected component 연결된 구성요소 : 분리된 모든 꼭짓점
4. Directed graphs
무방향 그래프 {u, v} 집합, 순서가 없음
방향이 있는 그래프 (u, v) 순서 중요
indegree 차수 ountdegree 외도
5. weighted graphs 가중치 그래프
모든 꼭짓점과 모든 모서리가 연결됨
Basic Graphs
1. Path Graph 꼭짓점 n개 모서리 n개 그래프 Pn

2. Cycle Graph 꼭짓점이 3개 이상 Cn

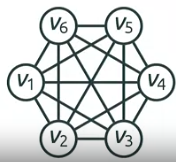
3. Complete Graph Kn 모든 모서리 연결 n(n-1)/2
4. 트리 : 순환이 없는 연결 그래프 n개 꼭짓점과 n-1개의 간선
모든 꼭짓점 쌍 사이에 고유한 경로가 있는 그래프

5. 이분법 : 모든 꼭짓점을 L과 R로 분할하여 모든 모서리가 L과 R의 꼭짓점을 연결할 수 있는 경우
순환그래프는 n이 홀수인 경우 빼고 이분법 가능
트리는 이분법 가능
coursera Introduction to Discrete Mathematics for Computer Science 과정 중
Graph Theory 1주차 내용 정리
'Fundamentals > Discrete mathmatics' 카테고리의 다른 글
| [이산수학] Combinatorics and Probability 조합론과 확률 수료증 (0) | 2023.09.19 |
|---|---|
| [이산수학] Combinatorics and Probability 조합론과 확률 5주차 (0) | 2023.09.19 |
| [이산수학] Combinatorics and Probability 조합론과 확률 4주차 (0) | 2023.09.19 |
| [이산수학] Combinatorics and Probability 조합론과 확률 3주차 (0) | 2023.09.13 |
| [이산수학] Combinatorics and Probability 조합론과 확률 2주차 (1) | 2023.09.13 |